esercizio Trovare l'equazione canonica dell'ellisse passante per i punti A(9/5,4) B(12/5,3) Devo prendere l'equazione canonica dell'ellisse x2 y2 ----- + ----- = 1 a2 b2 e sostituire alla x ed alla y i valori 9/5 e 4 (condizione di passaggio per il punto A) i valori 12/5 e 3 (condizione di passaggio per il punto B) Ottengo due equazioni nelle incognite a e b; risolvo e trovo i valori di a e b Condizione di passaggio per A(9/5;4) (9/5)2 42 ----- + ----- = 1 a2 b2 cioe' 81 16 ------- + ------ = 1 25a2 b2 Condizione di passaggio per B(12/5;3) (12/5)2 32 ----- + ----- = 1 a2 b2 cioe' 144 9 ------- + ------ = 1 25a2 b2 Devo quindi risolvere il sistema 81 16 ------- + ------ = 1 25a2 b2 144 9 ------- + ------ = 1 25a2 b2 Siccome la soluzione di questo sistema e' piuttosto complicata (e' un sistema di quarto grado) conviene ricorrere ad un artificio: Poniamo 1 --- = u a2 1 --- = v b2 Il sistema diventa 81u ------- + 16 v = 1 25 144 u ------- + 9 v = 1 25 e facendo il minimo comune multiplo 81 u + 400 v = 25 144 u + 225 v = 25       calcoli otteniamo 1 u = --- 9 1 v = ---- 25 quindi sostituendo le condizioni poste possiamo scrivere 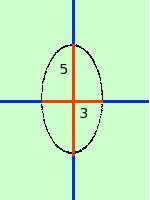a2 = 9        b2 = 25 e l'equazione dell'ellisse e' x2 y2 ----- + ----- = 1 9 25