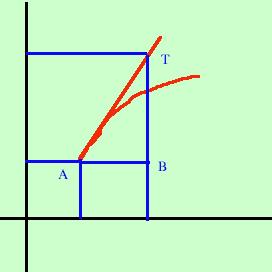
Differenziale di una funzione In parole molto povere il differenziale di una funzione non e' altro che l' incremento TB fatto sulla tangente invece che sulla curva; si ha TB ----- = m AB ora e' AB = dx m = f '(x) ponendo TB = df otteniamo df ---- = f '(x) dx che equivale a: df = f '(x)·dx Cioe' il differnziale di una funzione e' uguale alla derivata della funzione stessa moltiplicata per l'incremento dx 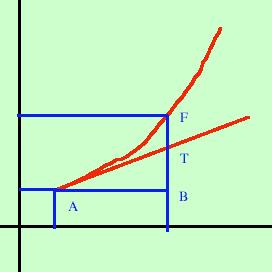Questa differenza FT fra il differenziale della funzione TB e l'incremento della funzione FB si puo' dimostrare che e' un infinitesimo di ordine superiore rispetto a dx (oppure h) e sara' poi usata per approssimare funzioni a livello locale mediante serie di funzioni: Serie di Taylor e Mac Laurin: BF = BT + TF f(x0 + h) - f(x0) = df + a(h) essendo a(h) = TF