sviluppo

sviluppo

Risolvere il seguente problema

In un rettangolo la somma delle dimensioni e' uguale al quintuplo della loro differenza, mentre se si aumentano di 4a le dimensioni il perimetro del rettangolo cosi' ottenuto diventa i 6/5 del precedente. Calcolare l'area del rettangolo

in un rettangolo i lati opposti sono uguali
le dimensioni di un rettangolo sono la base e l'altezza
A destra traccio la figura e scrivo l'ipotesi(hp) e la tesi(th)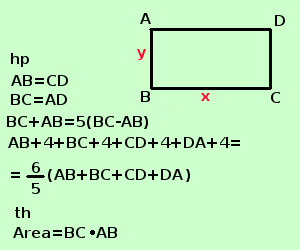

Per scrivere l'ipotesi scorro il testo e lo riscrivo in linguaggio geometrico:
rettangolo scrivo AB=CD e BC=DA
"la somma delle dimensioni e' uguale al quintuplo della loro differenza" scrivo AB+BC=5(AB-BC)
"se si aumentano di 4a le dimensioni il perimetro del rettangolo cosi' ottenuto diventa i 6/5 del precedente"
scrivo AB+4+BC+4+CD+3+DA+4=6/5(AB+BC+CD+DA)

La tesi dice che devo trovare l'area, per trovare l'area ho bisogno della base BC e dell'altezza AB
Come incognite, mi conviene indicare la base e l'altezza, una volta trovati i loro valori, moltiplicandoli trovero' l'area

BC=x
AB = y

"la somma delle dimensioni e' uguale al quintuplo della loro differenza" si scrive
x + y = 5(x - y)
x + y = 5x - 5y
4x - 6y = 0
2x - 3y =0

se si aumentano di 4a le dimensioni il perimetro del rettangolo cosi' ottenuto diventa i 6/5 del precedente" si scrive
x + 4 + y + 4 + x + 4 + y + 4 =6/5 (x + y + x + y)
2x+ 2y + 16 = 6/5 (2x + 2y)
5(2x + 2y + 16) = 6(2x + 2y)
10x + 10y + 80 = 12x + 12y
2x + 2y = 80
x + y = 40

Faccio il sistema

		2x - 3y =0
		x + y = 40

risolvo con il metodo di sostituzione, ricavo x dalla seconda equazione e lo sostituisco nella prima

		2(40 - y) - 3y = 0
		x = 40 - y

		80 - 2y - 3y =0
		x = 40 - y

		5y = 80
		x = 40 - y

		y = 16
		x = 40 - 16 = 24

		x = 24
		y = 16

quindi
AB = 16a
BC = 24a

ora posso trovare l'area
Area = BC·AB = 24a ·16a = 384a²

L'area vale 384a²