soluzione Risolvere il seguente problema In un rombo 1/4 della diagonale maggiore equivale ad 1/3 della diagonale minore , mentre la semidiagonale maggiore supera di 4 la semidiagonale minore; calcolare l'area del rombo 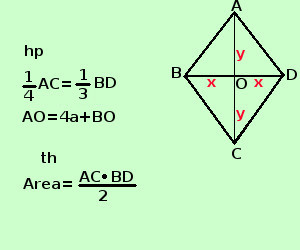Come incognite, per limitare le frazioni, mi conviene indicare le semidiagonali BD=2x B0 = OD = x AC = 2y AO = OC = y " 1/4 della diagonale maggiore equivale ad 1/2 della diagonale minore" si scrive 1/4·2y = 1/3·2x 3y = 4x "la semidiagonale maggiore supera di 4a la semidiagonale minore" si scrive y = 4a + x Faccio il sistema     3y = 4x     y = 4a + x     3·(4a + x) = 4x     y = 4a + x     12a = y     y = 4a + 12a     y = 12a     x = 16a     x = 16a     y = 12a quindi AO = 12a BO=16a AC = 24a BD = 32a ora posso trovare l'area Area = BD·AC /2 = 32a ·16a /2 = 256a2 L'area vale 256a2