sviluppo Risolvere il seguente problema In un rettangolo la somma delle dimensioni vale 4 volte la loro differenza, mentre se si aumentano le dimensioni di cm 2 il perimetro vale cm 72. Calcolare l'area del rettangolo Dimensioni di un rettangolo sono la base e l'altezza A destra traccio la figura e scrivo l'ipotesi(hp) e la tesi(th) 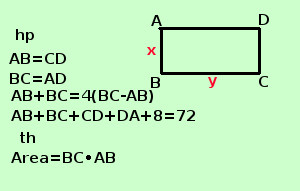Per scrivere l'ipotesi scorro il testo e lo riscrivo in linguaggio geometrico: rettangolo scrivo AB=CD e BC=DA "la somma delle dimensioni vale 4 volte la loro differenza" scrivo AB+BC=4(BC-AB) "se si aumentano le dimensioni di cm 2 il perimetro vale cm 72" i lati son 4, se aumento di 2 ciascuno in totale aumento di 8, quindi scrivo AB+BC+CD+DA+8=72 La tesi dice che devo trovare l'area, per trovare l'area ho bisogno della base BC e dell'altezza AB Come incognite mi conviene indicare la base e l'altezza, una volta trovati i loro valori , posso trovare l'area AB = CD = x BC = DA = y "la somma delle dimensioni vale 4 volte la loro differenza" si scrive x + y = 4(y-x) x + y = 4y - 4x 5x = 3y "se si aumentano le dimensioni di cm 2 il perimetro vale cm 72" si scrive x + 2cm + y + 2cm + x + 2cm + y + 2cm = 72cm 2x + 2y= 72 - 8 2x + 2y= 64 x + y= 32 Faccio il sistema     5x = 3y     x + y = 32 risolvo con il metodo di sostituzione, ricavo x dalla seconda equazione e sostituisco nella prima     5(32 - y) = 3y     x = 32 - y     160 - 5y = 3y     x = 32 - y     160 = 8y     x = 32 - y     y = 20     x = 32 - 20 = 12     x = 12     y = 20 quindi AB = 12cm BC = 20cm ora posso trovare l'area Area = BC·AB = 20cm ·12cm = 240cm2 L'area vale 240cm2