|
apprendimento Risolvere il seguente problema In un trapezio isoscele la base maggiore supera la minore di cm 40, mentre il lato obliquo supera di 5 cm la base minore. Sapendo che il perimetro vale cm. 130 trovare l'area del trapezio A destra traccio la figura e scrivo l'ipotesi(hp) e la tesi(th) 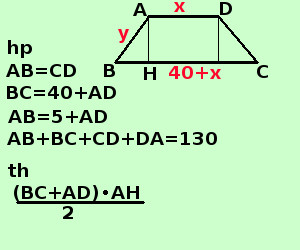
Per scrivere l'ipotesi scorro il testo e lo riscrivo in linguaggio geometrico trapezio isoscele AB = CD la base maggiore supera la minore di cm 40 BC = 40 + DA il lato obliquo supera di 5 cm la base minore AB = 5 * DA il perimetro vale 130 AB +BC + CD + DA = 130 area del trapezio (BC + DA)·AH /2 Scrivo il perimetro per esteso e ricordo che nel trapezio isoscele i lati obliqui sono uguali La tesi dice che devo trovare l'area: per trovare l'area di un trapezio servono le due basi e l'altezza con le relazioni che ho posso trovare le due basi ed il lato obliquo poi, considerando come e' fatto il trapezio isoscele, posso applicare il teorema di Pitagora per trovare l'altezza ad uno dei due triangoli uguali laterali Mi conviene indicare con x la base minore perche' compare piu' volte, come y prendo il lato obliquo AD = x BC = 40cm + x = 40 + x AB = CD = y rileggo il problema e lo traduco in linguaggio algebrico "la base maggiore supera la minore di cm 40" l'ho gia' usato per indicare BC " il lato obliquo supera di 5 cm la base minore" si scrive y = 5cm + x y = 5 + x "il perimetro vale cm 130" si scrive y + (40 + x) + y + x = 130 cm 2x + 2y = 130 - 40 x + y = 45
risolvo con il metodo di sostituzione
quindi AD = 20cm BC = 40cm + 20cm = 60cm AB = 25cm siccome ti chiede l'area devi trovare la misura dell'altezza. Se osservi il trapezio, considerando il triangolo AHB esso e' rettangolo e ne conosci 2 lati, perche' il lato obliquo l'hai trovato e la base AH puoi trovarla facendo la differenza fra la base maggiore e la minore e dividendo il risultato per 2 (essendo il trapezio isoscele i due triangolo laterali sono rettangoli e uguali) quindi .... |