sviluppo

sviluppo

Risolvere il seguente problema

In un rettangolo la base supera l'altezza di cm 10, mentre il perimetro vale cm 100: trovare l'area del rettangolo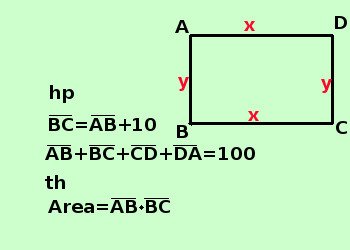

A destra traccio la figura e scrivo l'ipotesi(hp) e la tesi(th)

Per scrivere l'ipotesi scorro il testo e lo riscrivo in linguaggio geometrico:
rettangolo: ripasso mentalmente le proprieta'
la base supera l'altezza di 10 scrivo BC=10+AB
il perimetro vale 100 scrivo AB+BC+CD+DA=100

Scrivo il perimetro per esteso e ricordo che nel rettangolo i lati opposti sono uguali
La tesi dice che devo trovare l'area, per trovare l'area ho bisogno della base BC e dell'altezza AB
Come incognite mi conviene indicare la base ed l'altezza: una volta trovati i loro valori posso calcolare l'area
Ho 2 relazioni che posso coprire con 2 incognite x e y

Nota: sempre tante relazioni quante sono le incognite:
problemi a due incognite ti servono due relazioni;
problemi a 3 incognite ti servono 3 relazioni, eccetera

BC = DA = x
AC = BD = y

" la base supera l'altezza di cm 10" si scrive
x = 10cm + y
x = 10 + y

"il perimetro vale 100 cm" si scrive
x + y + x + y = 100 cm
2x + 2y= 100
x + y = 50

Faccio il sistema

		x = y + 10
		x + y = 50

risolvo con il metodo di sostituzione
sostituisco il valore di x nella seconda equazione

		x = y + 10
		y + 10 + y = 50

		x = y + 10
		2y = 40

		x = y + 10
		y = 20

sostituisco il valore di y nella prima equazione

		x =20 + 10
		y = 20

		x = 30
		y = 20

quindi:
BC = 30 cm
AB = 20cm

ora posso trovare l'area
Area = BC·AB = 30cm · 20cm = 600cm²

L'area vale 600 cm²