apprendimento Risolvere il seguente problema Dato il triangolo isocele ABC, sapendo che la base BC supera di cm 5 il lato obliquo e che il perimetro vale 80 cm trovarne l'area A destra traccio la figura e scrivo l'ipotesi(hp) e la tesi(th) 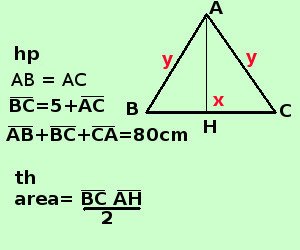Scrivo il perimetro per esteso e ricordo che nel triangolo isoscele i lati obliqui sono uguali La tesi dice che devo trovare l'area, per trovare l'area ho bisogno della base AB e dell'altezza CH Come incognite mi conviene indicare la base ed il lato obliquo, una volta trovati i loro valori, mediante il teorema di Pitagora, posso trovare l'altezza del triangolo e calcolare l'area BC = x AC = AB = y " BC supera di 5 il lato obliquo" si scrive x = 5 + y "il perimetro vale 80 cm" si scrive x + y + y = 80 cm x + 2y= 80 Faccio il sistema     x = 5 + y     x + 2y = 80 risolvo con il metodo di sostituzione     x = 5 + y     5 + y + 2y = 80     x = 5 + y     3y = 75     x = 5 + y     y = 25     x = 5 + 25     y = 25     x = 30     y = 25 siccome chiede l'area devo trovare la misura dell'altezza. Se osservo il triangolo, considerando il triangolo AHC esso e' rettangolo e ne conosco 2 lati: AH = AB/2= 15 cm AC = cm 25 applico il teorema di Pitagora al triangolo AHC HC2 = AC2 - AH2 = 625cm2 - 125cm2 = 400cm2 HC = √400cm2 = 20cm ora puoi trovare l'area