|
sviluppo Risolvere il seguente problema Dato il triangolo isocele ABC, sapendo che la base BC supera di cm 5 il lato obliquo e che il perimetro vale 80 cm trovarne l'area A destra traccio la figura e scrivo l'ipotesi(hp) e la tesi(th) 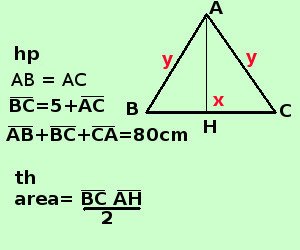
Per scrivere l'ipotesi scorro il testo e lo riscrivo in linguaggio geometrico: triangolo isoscele scrivo AB=AC supera di 5 il lato obliquo scrivo BC=5+AC il perimetro vale 80 scrivo AB+BC+CA=80 Scrivo il perimetro per esteso e ricordo che nel triangolo isoscele i lati obliqui sono uguali La tesi dice che devo trovare l'area, per trovare l'area ho bisogno della base AB e dell'altezza CH Come incognite mi conviene indicare la base ed il lato obliquo, una volta trovati i loro valori, mediante il teorema di Pitagora, posso trovare l'altezza del triangolo e calcolare l'area BC = x AC = AB = y " BC supera di 5 il lato obliquo" si scrive x = 5 + y "il perimetro vale 80 cm" si scrive x + y + y = 80 cm x + 2y= 80 Faccio il sistema
risolvo con il metodo di sostituzione
a differenza di quelli numerici il problema geometrico di solito non finisce trovando la soluzione del sistema: siccome ti chiede l'area devi trovare la misura dell'altezza. Se osservi il triangolo, considerando il triangolo AHC esso e' rettangolo e ne conosci 2 lati: se vuoi puoi considerare il triangolo CHB, e' lo stesso procedimento AH = AB/2= 15 cm AC = cm 25 applico il teorema di Pitagora al triangolo AHC HC2 = AC2 - AH2 = 625cm2 - 125cm2 = 400cm2 HC = √400cm2 = 20cm ora posso trovare l'area Area = BC·HC/2 = 25cm · 20cm/2 = 250cm2 L'area vale 250 cm2 Mi scuso, ma non so come indicare nel testo il segno di misura sui segmenti, so che e' un errore non farlo, quando fai il problema ricordati di metterlo tu |